バクテリア集団運動における秩序
アクティブ乱流:遊泳バクテリアの群れ運動
鳥の群れや魚の群れ、細胞集団に代表されるような、動き回る要素の集団のことをアクティブマターと呼び、非平衡統計力学の枠組みの中で研究が進められています[1,A]。我々はその中でも、水中を泳ぐバクテリアの群れに着目して研究をおこなっています。大腸菌や枯草菌に代表される、遊泳する棒状のバクテリアは、棒状の形状のために近隣のバクテリア同士が向きを揃えて進みます[2]。この排除体積相互作用の結果、高密度条件下で集団運動を示します。しかし、これらのバクテリアはべん毛で水の流れを作り出すことで泳いでいることから、流体相互作用も示します。この流体相互作用の結果、全体として大域的に向きの揃った状態は不安定となり、バクテリア集団の向きは長距離では揃わなくなります。この結果、局所的には個々のバクテリアの運動の向きは揃っているものの、全体としては揃っておらず、時空間的に速度場が乱雑に変動する集団運動を示します。この時空カオス的な集団運動を、バクテリア乱流あるいはアクティブ乱流と呼びます[3]。
渦格子秩序への自己組織化
カオス的な集団運動を示すバクテリア集団が、秩序だった振る舞いを示すことはあるのでしょうか? 生き物の集団や生体内での細胞集団などでは、秩序立った集団運動や統率のとれた運動が必要となることがあります。そこで、どのような条件下でバクテリア集団運動が秩序化するのかを調べるため、バクテリアの集団運動と境界条件の関係について調べました。
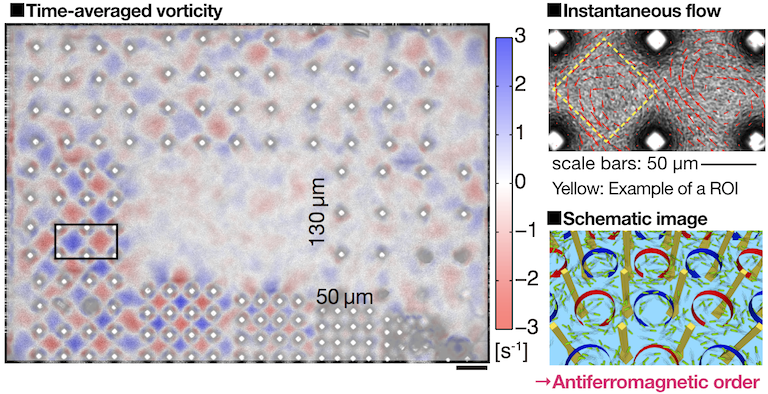
境界から遠く離れたバルク中のバクテリア乱流は、流体力学のNavier-Stokes方程式にバクテリアの泳ぐ力を加えた方程式で理解できることがわかっていたものの、その境界条件は自明ではなく、境界条件下でのバクテリア乱流の振る舞いを実験的に調査する必要がありました。我々は、微細加工技術により微小な柱の格子を構築し、そこにバクテリア乱流を流し込んで、その挙動を観察しました。直径20µm, 高さ150µmの柱を正方格子状に並べ、その正方格子の格子定数を50µmから130µmまで変化させて、同時観測を行いました(図1)。その結果、格子定数が70µm程度の正方格子において、バクテリア乱流が柱の合間で渦を形成し、隣同士の渦が逆回転する、反強磁性渦格子秩序が自発的に出現することを発見しました[3]。渦格子サイズを3×3から8×8まで変化させて測定をおこない、有限サイズの効果を定量的に評価することで、この渦秩序がシステムサイズ無限大の極限でも格子全体に渡り、時間的・空間的にも安定な長距離秩序であることを実験的に証明しました。これらの結果は、体積比でわずか4%程度の微小な拘束条件を課すだけで、カオス的なバクテリア集団運動に長距離秩序を生み出せることを意味しています。
最近では、この渦秩序の形成原理を実空間トポロジーにより理解することに成功しています[4]。実験的に、微小な柱がバクテリア乱流の流れ場のトポロジカル欠陥として振舞うことを見出しました。この性質は、柱が格子状に並んでいなくとも、単独の柱でも観測されました。さらに、柱がトポロジカル欠陥として機能するような新たな境界条件を実験的に見出し、連続場方程式によりマクロな渦秩序形成を再現することにも成功しました。この知見を応用することで、微生物集団から様々な渦秩序を抽出する一般論を構築しました。
参考文献
(当研究室)
[1] 集団運動の基礎理論に関する日本語解説記事: 西口大貴, 佐野雅己 “自己駆動粒子の集団運動 ~群れから始まる非平衡統計力学~” 雑誌 『数理科学』 2016年1月号 [pdf, web].
[2] D. Nishiguchi, K. H. Nagai, H. Chaté and M. Sano, Phys. Rev. E 95, 020601(R) (2017) [pdf, web].
[3] D. Nishiguchi, I. S. Aranson, A. Snezhko and A. Sokolov, Nat. Comm. 9, 4486 (2018) [web].
[4] H. Reinken, D. Nishiguchi, S. Heidenreich, A. Sokolov, M. Bär, S. H. L. Klapp and I. S. Aranson, Comm. Phys. in press (2020).
(他グループ)
[A] 最近の実験・理論に関するレビュー: M. Bär, R. Großmann, S. Heidenreich and F. Peruani, Annu. Rev. Cond. Matt. Phys. 11, 441 (2019) [web]; M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys. 85, 1143 (2013) [web].
主に関わっているメンバー
西口 大貴
