液晶乱流の界面成長に見るKPZ普遍法則
液晶乱流の界面成長とKPZ
平衡系における臨界現象の物理学は、様々な実験やIsingモデルの厳密解などが組み合わさって発展し、くりこみ群や共形場理論などの壮大な物理学体系が築かれるに至りました。では、同じような体系は非平衡に存在するのでしょうか? この答えはまだ誰も知りませんが、近年、Kardar-Parisi-Zhang (KPZ)クラス[A]と呼ばれる、ランダム界面成長を記述する非平衡普遍クラスに関して厳密な結果が数多く導出され、注目を集めています [1,B]。我々は、液晶に電圧をかけて乱流状態を生成し、その成長過程を調べて、KPZクラスに関する厳密解と直接比較可能な実験結果をあげています。
我々が観察する乱流状態はDSM2と呼ばれ、液晶の位相欠陥からなっていて、十分な電圧のもとで紫外レーザーを打ち込むことで生成します。この際、ビーム形状を変えることで、円形の界面も平面状の界面も作れます(ムービー1、2)。
界面ゆらぎの普遍法則と界面形状依存性:KPZ普遍サブクラス
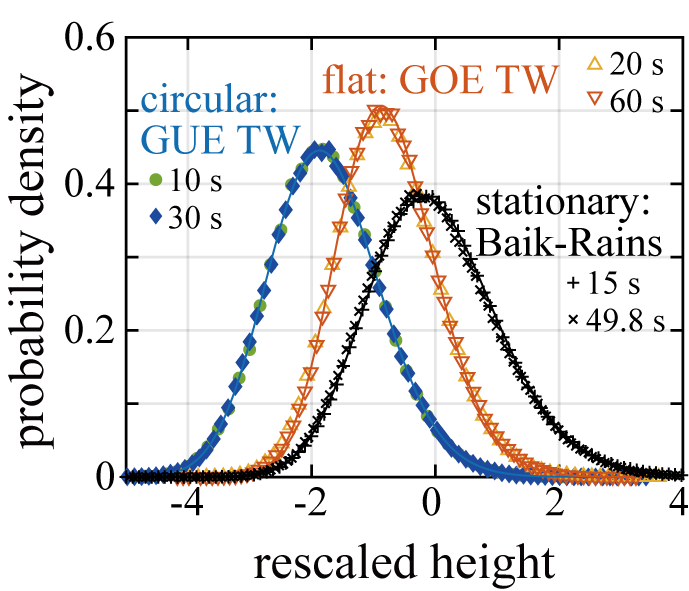
円形界面・平面界面のそれぞれの場合について界面ゆらぎの統計的性質を測定した結果、どちらもスケーリング指数はKPZクラスのものでありながら、ゆらぎの分布や相関関数は互いに異なる関数形を示すことがわかりました。得られた関数形はKPZクラスに属する可解模型の厳密解の結果[1,B]と一致しており、特に分布関数は、GUEやGOEと呼ばれるランダム行列の最大固有値分布(Tracy-Widom分布)と同じものが現れます(図1)。このことから、分布や相関といった詳細な性質にも普遍性が成り立つことがわかり、さらに、KPZクラスは界面形状(あるいは初期条件)に応じていくつかの「普遍サブクラス」に分離するという興味深い結論が得られます[2,3]。
理論的には、円形界面・平面界面に加えて、定常界面が代表的な3つのサブクラスとして知られています[1,B]。定常界面は、無限系で無限時間経過後に行き着く状態であるため、直接検証は困難でしたが、我々は後に述べるホログラフィ実験系により、定常界面の形状を直接生成することによって、定常界面の時間発展に関する非自明な統計法則の直接検証に成功しました[4]。特に、定常界面の特徴的な高さゆらぎ分布とされていた Baik-Rains分布(図1)や、2点相関関数に関するPrähofer-Spohn厳密解の検証に成功し、代表的なサブクラス全てに対して実験的裏付けを与えることができました。
KPZクラスの数理的研究は大変進んでいますが、それでも時間相関をはじめとして、まだ解けていない統計的性質が数多く存在します。我々は液晶乱流実験によって、そうした未解決ながらも普遍的な諸性質を高精度で決定しています。特に、時間相関に関しては、円形界面と平面界面で、ゆらぎの正負の対称性や相関の持続性に質的な違いが現れることを発見しました[3]。円形界面では、ゆらぎの相関が無限に持続するという特異な性質を実験で見出しましたが、これはのちに理論的にも確認され[5]、ついには数学の定理も作られました[C]。
初期条件を任意にデザイン可能な、ホログラフィ実験系の製作
KPZ普遍法則は、界面形状によっていくつかの「普遍サブクラス」に分類され、界面形状を決めるのは主として初期条件です。そこで我々は、液晶乱流の生成に用いる紫外レーザーに、レーザーホログラフィ技術を組み合わせることで、界面の初期形状を任意にデザインできる実験系を製作しました(ムービー3)[6]。
この実験系を使うと、従来は調べることができなかった様々な界面形状で、KPZゆらぎの普遍的な性質を調べることができます。例えば、有限の半径の円を初期条件とすると、円から外向きに成長する界面と、内向きに成長する界面が現れます。我々は、実験と数値計算の両面から、外向きの成長界面は平面界面サブクラスから円形界面サブクラスへのクロスオーバーを示すこと、内向きの成長界面は平面サブクラスの性質を示したあと、円の中心点付近で潰れるまで円形界面の性質は示さないことを見出しました[6]。
理論的には、任意の初期条件のもとでの界面ゆらぎを計算する手法として、変分公式が提案され[D]、厳密解研究で活用されています。我々は、変分公式を数値的に評価する方法を提案し、それによって実験や数値計算の結果を定量的に再現できることを示しました[6]。本成果により、変分公式が、厳密解の計算だけでなく、任意の初期条件のもとでの界面成長の統計的性質を予言したり説明したりするのに使えることが明らかになりました。
KPZ半空間問題
界面が何らかの境界で仕切られているとき、その境界条件は、界面の統計的性質に影響を及ぼすと考えられます。理論的には、半無限空間 $x \geq 0$ で界面が成長する場合の、境界 $x=0$ 近傍の界面ゆらぎの性質がよく調べられており、界面形状や境界条件に応じて、いくつかの普遍サブクラスが確立されています。特に、円形界面が、 $x=0$ で十分に正の傾きをもつような境界条件のもとで成長するときは、$x=0$ではランダム行列理論のGSE Tracy-Widom分布が予言されており、半空間KPZも極めて魅力的な数学的構造を有しています。しかしながら、実験的にNeumann境界条件などの境界条件を課すことは困難で、半空間KPZの実験検証は非現実的課題と思われる状況でした。
そこで我々は、半空間KPZと同等の対称性が期待できる現実的な設定として、左半分と右半分で界面成長速度が異なる、二領域界面成長問題を提案しました[7](ムービー4)。実験的には、まだGSE Tracy-Widom分布等の検証には至っていませんが、数値計算では半空間KPZで期待される各種の普遍分布が明瞭に観測され[7]、半空間KPZの実験研究に、二領域界面成長が極めて有効な設定であろうことが明らかになりました。
参考文献
(当研究室)
[1] KPZ厳密解研究に関する入門的レビュー: K. A. Takeuchi, Physica A 504, 77 (2018) [web, preprint].
[2] K. A. Takeuchi and M. Sano, Phys. Rev. Lett. 104, 230601 (2010) [pdf, web]; K. A. Takeuchi, M. Sano, T. Sasamoto, and H. Spohn, Sci. Rep. 1, 34 (2011) [pdf, web].
[3] K. A. Takeuchi and M. Sano, J. Stat. Phys. 147, 853 (2012) [web, preprint].
[4] T. Iwatsuka, Y. T. Fukai, and K. A. Takeuchi, Phys. Rev. Lett. 124, 250602 (2020) [pdf, web].
[5] J. De Nardis, P. Le Doussal, and K. A. Takeuchi, Phys. Rev. Lett. 118, 125701 (2017) [pdf, web].
[6] Y. T. Fukai and K. A. Takeuchi, Phys. Rev. Lett. 119, 030602 (2017) [pdf, web]; Phys. Rev. Lett. 124, 060601 (2020) [pdf, web].
[7] Y. Ito and K. A. Takeuchi, Phys. Rev. E 97, 040103(R) (2018) [pdf, web].
(他グループ)
[A] A.-L. Barabási and H. E. Stanley, Fractal Concepts in Surface Growth (Cambridge Univ. Press, Cambridge, 1995).
[B] KPZ厳密解研究に関する他の代表的レビュー: T. Kriecherbauer and J. Krug, J. Phys. A 43, 403001 (2010) [web]; I. Corwin, Random Matrices Theory Appl. 1, 1130001 (2012) [web]; H. Spohn, Lecture Notes of the Les Houches Summer School, 104, 177-227 (2017) [web, preprint].
[C] K. Johansson, Probab. Theory Relat. Fields 175, 849 (2019) [web].
[D] J. Quastel and D. Remenik, Springer Proceedings in Mathematics & Statistics, 69, 121 (2014) [web, preprint].
主に関わっているメンバー
竹内 一将、深井 洋佑、伊藤 康文、岩塚 崇泰
